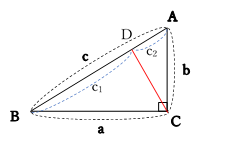
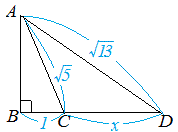
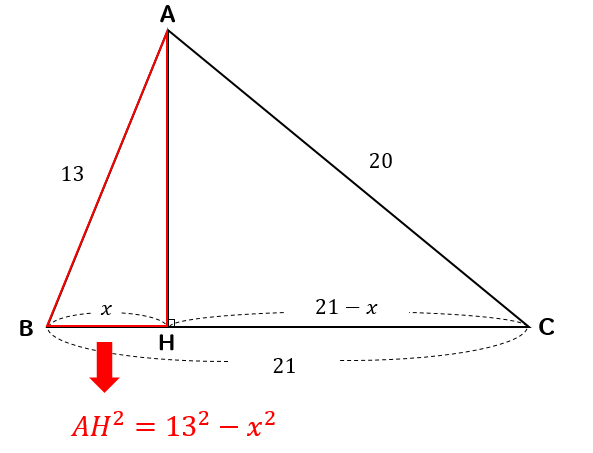
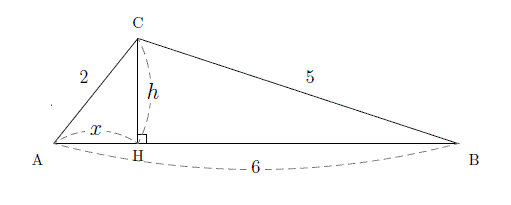
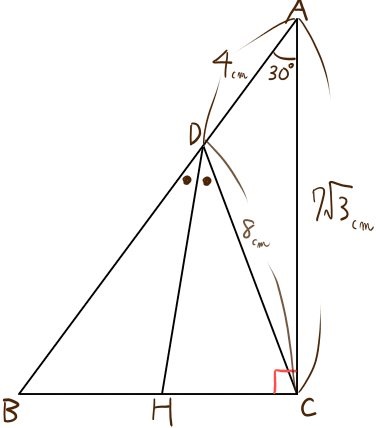
例3 右図で AC の長さは三平方の定理で求められるが, さらに相似図形の性質を使えば, ACBC=ABx になるので, x が求められる. (相似図形の性質をまだ習っていないときは こちらを先に 読む) 直角三角形 ABC に三平方の定理を適用すると 2152=AC2 AC2
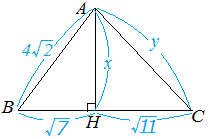
三平方の定理 問題 答え 付き- でも、大丈夫。 三平方の定理(ピタゴラスの定理)を使えば求められるんだ。 DFの長さをxcmとして、三平方の定理(ピタゴラスの定理)に代入してみると、 13² = 5² x² x = 12 あら不思議! 長さがわからない直角三角形の辺を求めることができたねAB=17cm, AC=10cm, BC=21cmの三角形 A B C 図は1辺4cmの正六角形である。 面積を求めよ。 図は一辺10cmの正八角形である。 面積を求めよ。 解説リクエスト 三平方の定理とは 三平方の定理 (基本問題1) 例題と練習 三平方の定理 (基本問題2) 例題と練習 三平方の
三平方の定理 問題 答え 付きのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  |  |
 |  | |
 |  | |
「三平方の定理 問題 答え 付き」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
 | 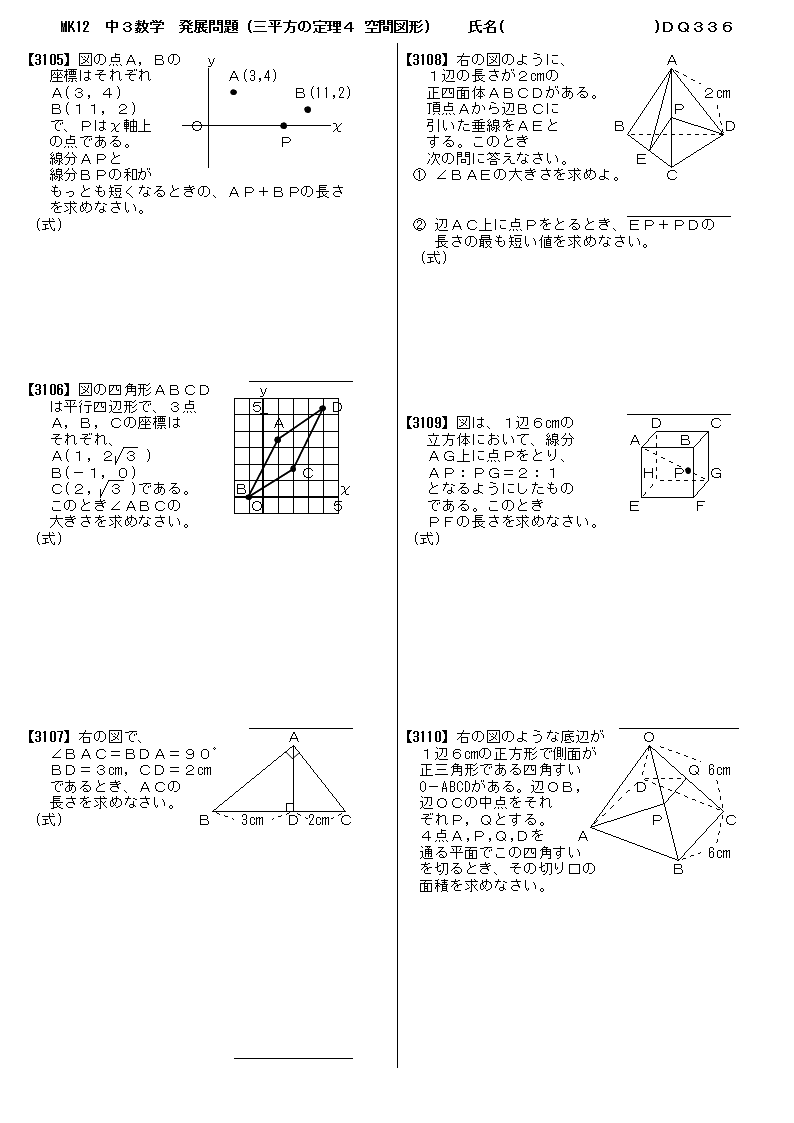 | 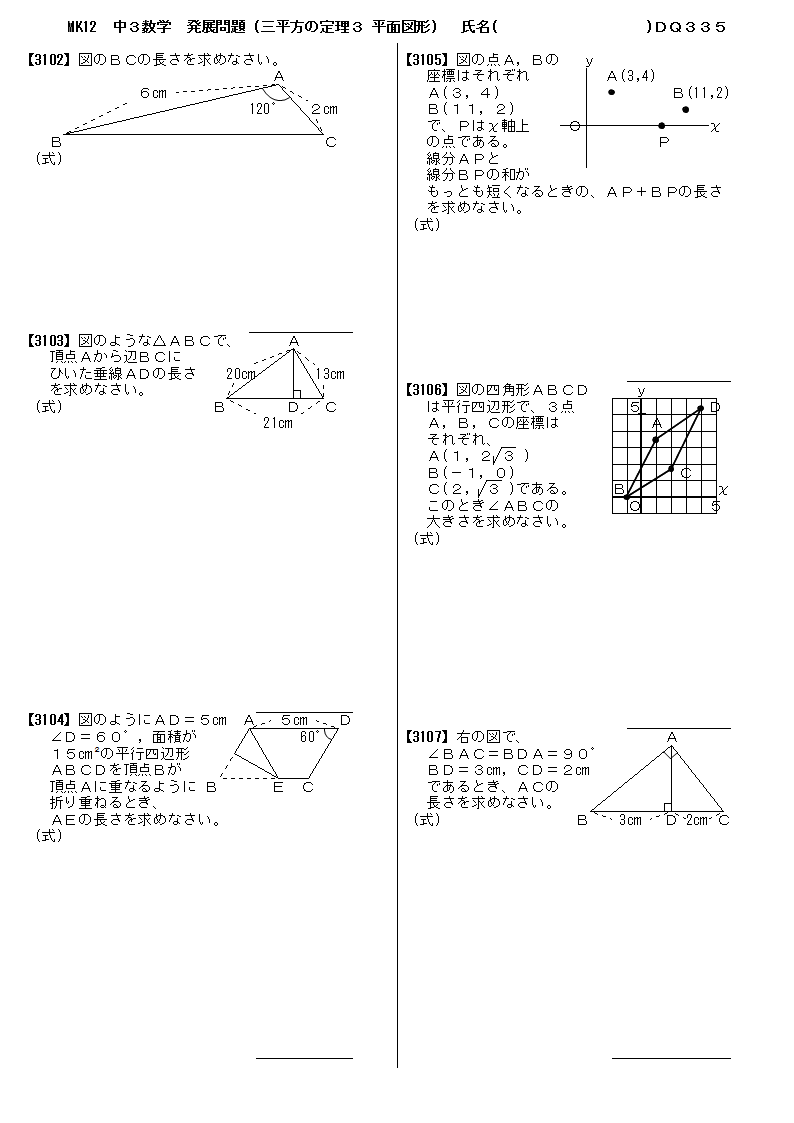 |
「三平方の定理 問題 答え 付き」の画像ギャラリー、詳細は各画像をクリックしてください。
 | 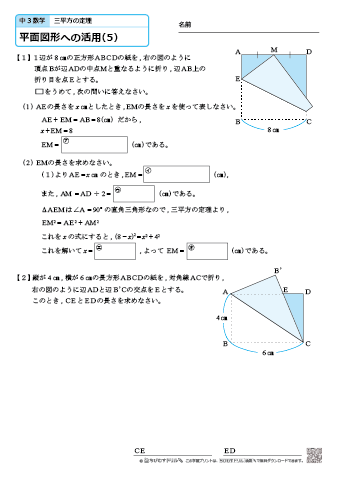 | |
 | ||
 | 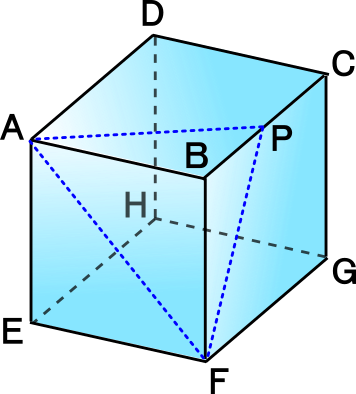 |  |
 |  |  |
「三平方の定理 問題 答え 付き」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 | ||
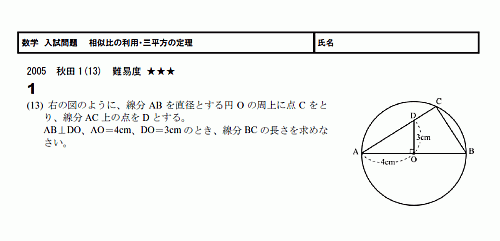 | 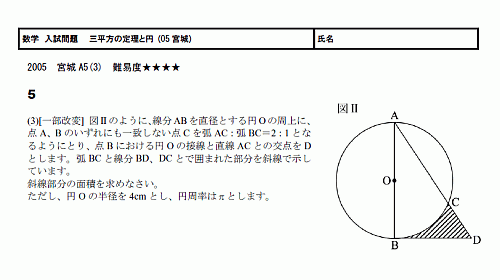 | |
「三平方の定理 問題 答え 付き」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
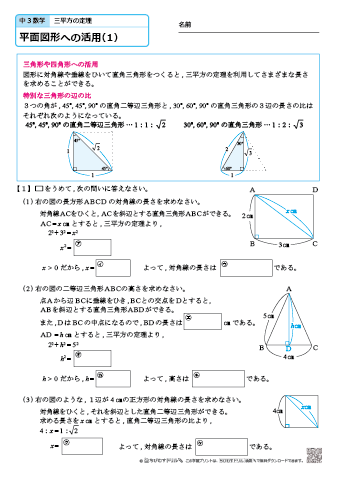 | ||
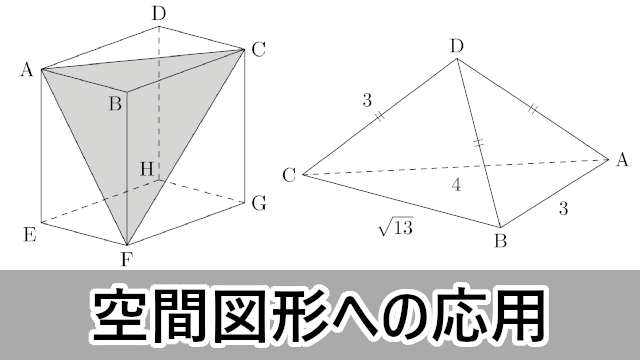 |  | |
 |  |  |
「三平方の定理 問題 答え 付き」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
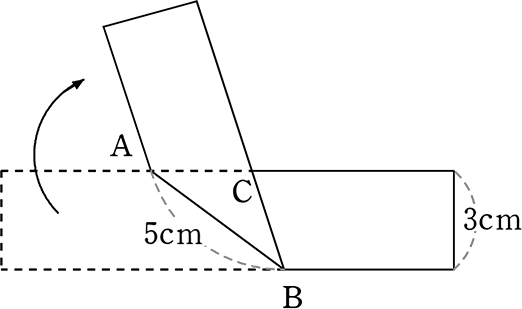 | 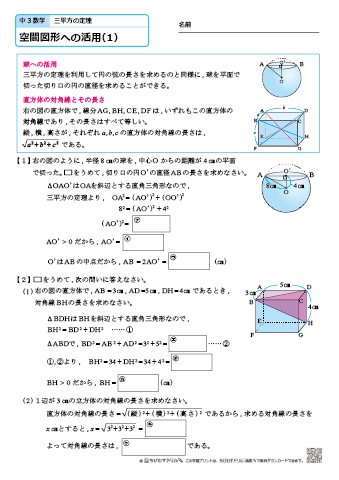 |  |
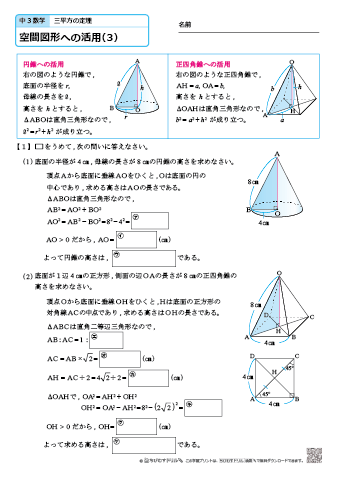 | ||
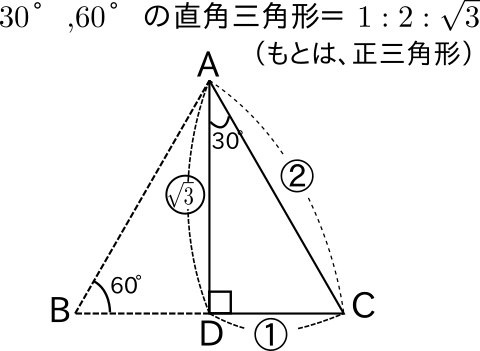 | ||
「三平方の定理 問題 答え 付き」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  | |
 |  |  |
「三平方の定理 問題 答え 付き」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
 |  |  |
「三平方の定理 問題 答え 付き」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
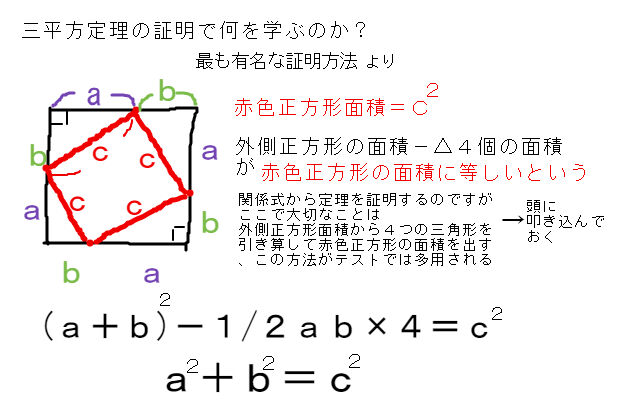 |  |
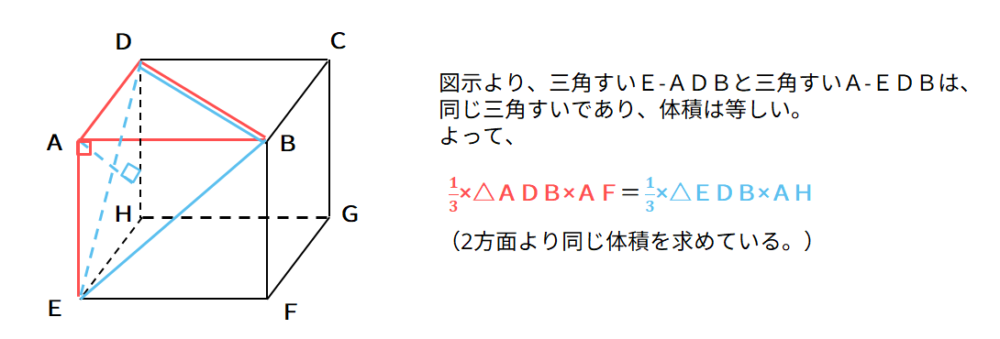
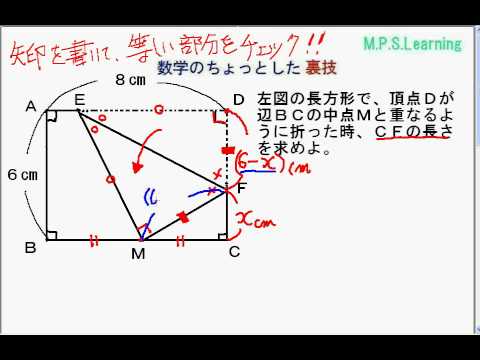
中学数学の三平方の定理3練習問題です。授業の予習、復習から定期テスト対策、受験勉強に活用してください。 この直角三角形で三平方の定理を使う。 oo'=17, ac=bo'=5, oa=3, つまりoc=8 よってco' 2 8 2 =17 2 計算するとco'=15 co'=abなので ab=15 a b o o' c 3辺の比に平方根(ルート)が含まれますが、暗記しておけば簡単に計算できます。 三平方の定理の応用問題 基本問題が解けたところで、応用問題にも挑戦してみましょう。 テストや入試では、最初から直角三角形が与えられるわけではありません。
Incoming Term: 三平方の定理 問題 答え 付き, 数学 三平方の定理 問題 難しい, 中3 数学 三平方の定理 問題, 三平方の定理 30度 60度 90度, 三平方の定理 30 60 90, 三平方の定理 計算 30 60, 三平方の定理 証明 中学生 簡単, 三平方の定理 証明 中学生 レポート, 中3 数学 三平方の定理 難問, 三平方の定理 計算 角度 底辺,




0 件のコメント:
コメントを投稿